
In order to maximize profitability while complying with government regulations regarding net package contents, food manufacturers and packagers must achieve an optimal balance.
Consistent overfilling to minimize risk is inefficient and sacrifices profitability, while aggressive filling practices result in significant risks of non-compliance with net contents regulations leading to potential penalties, loss of reputation, and impaired customer relations.
Statistical process control and process capability methods may be utilized to determine optimal targets for product fill weights or volumes for a given process. Subsequent focused efforts to minimize variation will allow the target to be further optimized, resulting in less waste without compromising risk.
U.S. Regulatory Requirements
The specific regulatory requirements for net contents of foods vary by country. This article will address the basic U.S. regulations although the methods are easily applied to variations of these regulations.
The National Institute of Standards and Technology (NIST) Handbook 133, “Checking the Net Contents of Packaged Goods” has become a widely adopted standard for evaluating net package contents. The standard includes two basic requirements. The first applies to the average net quantity of contents in each lot and the second applies to each individual package. Although “net quantity of contents” could refer to weight, volume, count, or other measure, we will simply use weight for the remainder of this paper. The two basic requirements are:
- The average net weight of packages in a lot must at least equal the label declared net weight.
- Any individual package net weight must not be less than the label declared net weight by an amount that exceeds the Maximum Allowable Variation (MAV). (The MAV depends on the label weight. Handbook 133 provides MAV values for various label weight ranges.)
Random lot sampling has been used historically to evaluate the likelihood that a given lot meets requirements and Handbook 133 contains sampling plans for these inspection procedures. Some sampling plans (with large lot and sample sizes) permit at most one package that exceeds the MAV. This acceptance sampling approach to quality control is reactive rather than preventative. Progressive companies have moved to real time statistical process control to proactively achieve consistent and predictable process performance. When applied properly, SPC can help to prevent production of unacceptable product.
Estimating Risk of Non-Compliance (Exceeding MAV)
The procedure for estimating the risk of non-compliance will be illustrated with an example. The process under study fills up packages of crumbled feta cheese and the declared net weight (DNW) on the label is 24 oz (or 680 g). From Handbook 133, the MAV is found to be 25.4 g based on the package weight. Thus, the lowest allowable value for an individual container is 680 – 25.4 = 654.6 g. This lower limit will be referred to in this paper as LMAV.
Since any estimate of process capability (or risk of non-compliance) is meaningless if the process isn’t stable, we first assess the stability with appropriate control charts (see previous articles for various control charting topics).
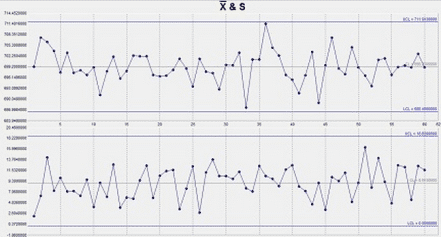
The above chart is an X-bar & S chart for feta cheese weights. It shows that the process is stable (i.e. in control). Please note that as the top chart above plots averages, it tells us nothing about whether the individual packages are in compliance or not. The purpose of control charts is only to assess stability and provide a signal when significant process changes occur. Control charts should never be used to infer process capability.
It may also be shown that the above data is well described by a normal distribution using a normality test (more on non-normal data later). From the data collected, the process average is estimated to be 699.2 g and the standard deviation is estimated to be 9.5 g. The average package is overfilled by 19.2 g.
The graphic below shows the estimated distribution of cheese weights with the DNW and MAV also indicated.
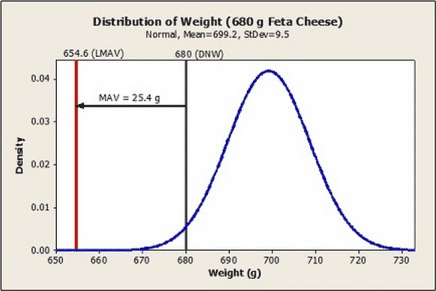
The risk of producing a package with a weight below 654.6 (the lowest allowable weight for an individual package or LMAV) is simply the area under the curve to the left of 654.6. This is easily found by computing the Z-value for the LMAV.
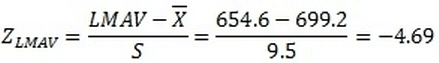
The Z value represents the number of standard deviations that LMAV is below the process average. With the Z value, the standard normal table will provide the area beyond 4.69 standard deviations. The result is 0.0000014 which is the probability that a random unit will be non-compliant. This equates to 0.00014% or 1.4 units per million and represents the risk of non-compliance for the MAV requirement.
Here, the risk is low and the company appears to have a significant opportunity to reduce raw material costs by simply shifting the process average closer to the DNW. For example, shifting the process average from 699.2 g to 690 g would change the Z value to -3.73 resulting in a probability of 0.000096 or 0.0096% or 96 per million.
Determining Target Weight
It should be clear that we may fix our risk at a tolerable level and compute the process average that would result in the specified risk level. The risk criterion is typically specified as the percentage of individual packages that would be expected to fall below the LMAV. Some producers prefer to establish the percentage of packages (e.g. 30%) that are expected to fall below the DNW (although this does not necessarily provide protection against non-compliance for the MAV requirement).
In order to compute the target for a specified risk of an individual unit falling below the LMAV, we can simply re-arrange the above formula for the Z-value and replace the process average with the target.

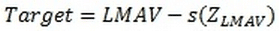
Here, we’ll illustrate the target weight calculation with the feta cheese example. Suppose management has decided that a 0.2% chance of a package exceeding the MAV is a tolerable risk.
We need to find the Z value associated with an area below the LMAV of 0.002. The approximate Z value may be found using the Z table but the Excel function “NORMSINV” may be used to find the Z value of -2.878. This means that the area under curve beyond 2.878 standard deviations is 0.002 (0.2%). We have:

Thus, we are able to reduce the process average by 17.3 g (from 699.2 to 681) which reduces the amount of overfill to 1.9 g. A considerable material savings may be realized while still having a low risk of exceeding the MAV requirement.
Recall that the other basic requirement is that the process average must at least be equal to the DNW. In our example, the DNW is 680 g so our computed target value is only about 2 grams above the required process average. If we elected to center the process at 681.9 g, the control chart would need to be designed with a sufficient sample size to detect about a 2 gram process shift in order catch a violation of the average requirement. The sample size required in this example to detect a 1/5th sigma shift would be prohibitively large. (See the articles “How should the Sample Size be Selected for an Xbar Chart” – Parts I and II.)
Optimizing the Process by Reducing Common Cause Variation
Excessive common cause variation directly affects material costs and the bottom line. By systematically determining sources of variation and addressing them, immediate savings may be realized. Design of Experiments is an invaluable method for understanding which factors and interactions between factors affect process variability. Using efficient experimentation, a model that predicts variability may be developed and factor settings that minimize variation may be identified.
Reducing variation allows the process target to be established closer to the DNW while controlling the risk of exceeding the MAV requirement to a tolerable level. Furthermore, when variation is reduced, it is much easier to control the process as smaller process shifts are detectable for a given sample size. Since small process shifts can be detected, the process target may be established closer to the DNW thus driving down material usage and costs.
To illustrate, suppose the standard deviation of our feta cheese filling process was reduced from 9.5 g to 3 g and the target was determined to be 685 g. The target was determined based on the need to achieve a reasonably low risk of an individual package exceeding the MAV and the need to efficiently detect a potential process shift of 5 g which would lead to a violation of the average requirement. (A sample size of 7 packages would be needed to detect a shift of 5 units with 92% probability on the first sample following the shift.)
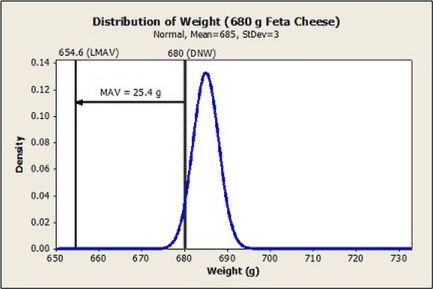
The improved process (centered at 685 g) results in an average overfill of only 5 g. As compared to the original process, we have reduced variation and shifted the process average closer to the DNW. There is negligible risk of an individual package exceeding the MAV and the process can be efficiently controlled to detect process shifts that would risk the ability to meet average requirement.
The reduction in overfill of an average package is 14.2 grams (about one half ounce). If the company produces 10 million packages of feta cheese per year and the ingredients per pound of feta produced amount to $2.50 (or $0.156 per ounce), the annual savings would amount to $780,000!
Process Capability for Non-Normal Data
While non-normal (e.g. skewed) data does not present an issue for SPC charts of averages (thanks to the Central Limit Theorem), process capability methods (that utilize individual measurements) are sensitive to the underlying distribution. The methods and equations utilized above for determining the proportion of non-compliant packages and target weights assume that the individual package weights are well described by a normal distribution.
If the normality assumption is unjustified (based on a normality test), then non-normal methods must be employed. Specifically, a more appropriate distribution may be fit to the data, and that probability distribution may be used to set weight targets that properly control the risk of non-compliance.
Summary
This paper illustrated the use of Statistical Process Control and Process Capability methods for optimizing product target weights given the inherent tradeoffs between minimizing overfills and minimizing risks of non-compliance to government regulations. Excessive variability leaves potential savings unrealized, so additional statistical methods to attack variation should be deployed to achieve optimal results.
Steven Wachs, Principal Statistician
Integral Concepts, Inc.
Integral Concepts provides consulting services and training in the application of quantitative methods to understand, predict, and optimize product designs, manufacturing operations, and product reliability. www.integral-concepts.com